Математическое моделирование систем, описываемых обыкновенным дифференциальным уравнением при заданных начальных условиях, осуществляется наиболее просто, если уравнение в явном виде разрешено относительно производной:
От влияния внутренних параметров h и воздействий внешней среды v можно избавиться, повторяя решение заданного уравнения при фиксированных значениях этих параметров h=const, v=const.
Рассмотрим дифференциальное уравнение первого порядка
(2)
Если требуется найти интегральную кривую у=у (х), проходящую через заданную точку М0 (х0, у0), то формулируется задача Коши: найти решение у=у(х) уравнения, удовлетворяющее начальному условию у(х0)=у0.
Существуют различные приемы решений такой задачи: метод последовательных приближений, интегрирование уравнений с помощью степенных рядов, методы Адамса, Крылова, Милна и др. Ниже рассмотрены методы Эйлера и Рунге-Кутта, первый из которых является наиболее наглядным, а второй – наиболее популярным.
Метод Эйлера и его модификации
Принцип численного решения уравнения (2) при начальном условии у(х0)=у0, основанный на методе Эйлера, чрезвычайно прост. Он непосредственно вытекает из смысла производной. Подставляя заданное начальное значение х0 и у0 в правую часть Исходного уравнения (2), мы определим производную в этой точке: y'(х=х0)=f(х0, у0), т. е. найдем тангенс угла наклона касательной к искомой кривой. Это дает возможность определить приближенное значение функции в соседней точке при x1 =x0 + h (рис. 2). При этом приращение функции будет 
, а полное значение ординаты при этом составит 
. Таким образом, получены приближенные координаты соседней точки x1, y1, принимая которые за исходные, мы можем повторить вычисления методом Эйлера и найти следующую точку с координатами х2, у2. Аналогично вычисляются все последующие точки по формулам
(3)
где h – достаточно малый шаг приращений координаты х.
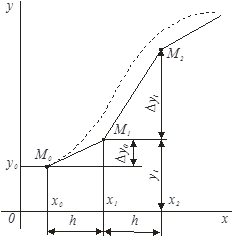
Рис. 2.К решению уравнения методом Эйлера
Для того чтобы назначить величину шага, обеспечивающую необходимую точность вычислений, расчет повторяют при шаге, в два раза меньшем первоначального. Если разница в результатах вычислений превышает требуемую точность, то шаг разбиения уменьшают еще раз и повторяют расчет.
Метод Эйлера приводит к систематическому накоплению ошибок, поэтому в практике расчетов используют модификации этого метода: метод ломаных и метод Эйлера-Коши.
В первом случае сначала вычисляют промежуточные значения
и находят направление поля интегральных кривых в средней точке
, а затем полагают 
.
Во втором случае грубое приближение
, 
уточняется следующим образом:
Дальнейшим развитием и уточнением метода Эйлера являются различные схемы метода Рунге-Кутта. Ниже рассмотрена одна из таких схем, получившая наибольшее распространение.
Метод Рунге-Кутта
Основная схема метода Рунге-Кутта имеет вид:
(4)
где
(5)
(i = 1, 2,…, n).
Для определения правильности выбора шага h выполняют двойной пересчет, как это было отмечено при рассмотрении метода Эйлера.
Приближенное решение ДУ n-го порядка при заданных начальных условиях
Для дифференциального уравнения n-го порядка
(6)
задача Коши состоит в нахождении решения
удовлетворяющего начальным условиям
; 
; …; 
где x0, y0, yo’… - заданные числа. Такая задача может быть приведена к решению системы дифференциальных уравнений путем подстановок
, 
, …, 
(7)
Будем иметь:
(8)
Дальнейшее решение задачи выполняют как указано выше, например, методом Рунге-Кутта.
Для примера найдем приближенное решение нелинейного дифференциального уравнения свободных колебаний маятника в среде, обладающей сопротивлением. Пусть 
– угол отклонения маятника от положения равновесия, t – время. Полагая, что сопротивление среды пропорционально угловой скорости маятника, имеем для = (t) нелинейное дифференциальное уравнение второго порядка
(9)
где 
– коэффициент затухания колебаний;
g – ускорение свободного падения;
l – длина маятника.
Принимая =0,2, g/l= 10, приходим к уравнению
(10)
с начальными условиями: угол отклонения 
, угловая скорость 
.
Выполняя подстановки типа (9), т.е. полагая 
, запишем уравнение (10) в виде системы уравнений
Скачать реферат