Идея метода конечных элементов (МКЭ) заключается в том, что вместо поиска единого аналитического представления функции v используют ее кусочно-линейную аппроксимацию, т.е. всю область решения разбивают на подобласти конечных размеров, достаточно малых, чтобы обеспечить требуемую точность линеаризации.
Рассмотрим основы МКЭ на примере одномерной задачи, точное решение которой описывается кривой, изображенной на рис. 1, а. Прежде всего разбейте область 
на конечные элементы 
и т. д. В пределах длины каждого элемента искомую функцию можно считать линейной (рис. 1, б):
. (2)
Если тем или иным способом вам удастся определить значения искомой функции 
в узлах
, то задача будет решенной, поскольку с учетом равенства (2) вы получите возможность вычислить приближенные значения функции в любой точке. Рассмотрим, как можно определить значения искомой функции в узлах .
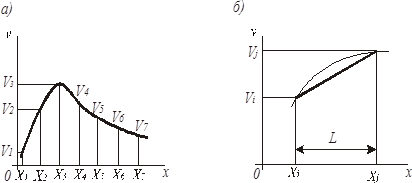
Рис. 1.Одномерные конечные элементы
Узловые значения функций вы можете искать различными способами, исходя из физического смысла задачи. Задача может быть задана в форме дифференциальных уравнений, либо в виде некоторого функционала 
. В первом случае удобно воспользоваться методом Бубнова – Галеркина, минимизируя ошибку приближенного решения, во втором – каким-нибудь вариационным принципом, обеспечивающим минимизацию функционала. Используя кусочно-линейное представление функции и записывая функционал в виде 
, вы обеспечите реализацию минимума энергии, приравнивая нулю частные производные:
В результате будет получена система уравнений
решение которой позволит вычислить вектор 
, т.е. найти значения искомой функции в узлах и тем самым решить задачу.
Унификация вычислительных процедур накладывает некоторые особенности на реализацию МКЭ, для уяснения которых вновь обратимся к решению одномерной задачи (рис. 1).
В общем случае алгоритм МКЭ состоит из четырех этапов:
1) выделение конечных элементов (разбиение заданной области на конечные элементы);
2) определение аппроксимирующей функции для отдельного конечного элемента (определение функции элемента);
3) объединение конечных элементов в ансамбль;
4) определение вектора узловых значений функции.
Первый этап. Первый этап расчета с использованием МКЭ состоит в разбиении области на конечные элементы. Такое разбиение начинают обычно от границы области, стараясь наиболее точно повторить ее конфигурацию, затем производят разбиение внутренних областей. Сначала выделяют достаточно крупные подобласти, которые отличаются по свойствам материала, геометрии, напряженному состоянию и пр. Затем каждую подобласть разбивают на конечные элементы принятой формы, чаще всего треугольные, при этом размеры конечных элементов могут быть приняты различными (рис. 2) в зависимости от требуемой точности описания. Резкого изменения размеров конечных элементов на границах подобластей стараются избегать.
Важное значение имеет нумерация узлов конечных элементов. Дело в том, что матрицы коэффициентов систем алгебраических уравнений в МКЭ представляют собой сильно разряженные матрицы ленточной структуры. Ненулевые элементы таких матриц располагаются параллельно главной диагонали, при этом ширина полосы зависит от числа степеней свободы узлов и их нумерации (от разности номеров соседних узлов). Выбор оптимальной нумерации узлов способствует существенному сокращению затрат вычислительных ресурсов компьютера.
Информация о разбиении области на конечные элементы и нумерации узлов является исходной для последующих этапов расчета. Обычно требуется указывать тип конечного элемента, его порядковый номер, номер узла сети, координаты этого узла, значения физических параметров в пределах конечного элемента и др. Такая топологическая информация обычно содержит примерно в шесть раз больше чисел, чем количество узлов сетки разбиения. Для объектов средней сложности объем такой информации измеряется сотнями тысяч. Понятно, что ручной ввод этой информации, помимо чрезвычайной утомительности, может сопровождаться ошибками.
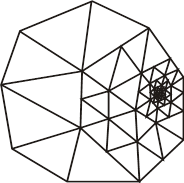
Рис. 2. Пример разбиения подобласти на конечные элементы
Процедуры по вводу информации оптимальной нумерации узлов удается формализовать, что позволило разработать специальные программы, называемые препроцессорами, которые либо существуют в виде автономных программ, либо непосредственно включаются в состав программных комплексов, реализующих МКЭ.
В данном примере суть его понятна без пояснений: выделено шесть конечных элементов 
в общем случае разных по длине.
Второй этап. Рассмотрим (рис. 1, б) один из выделенных элементов 
(одномерный симплекс-элемент). Для определения коэффициентов а и b полинома (2) запишем граничные условия:
при 
при 
Подставляя эти значения в равенство (2), получим систему двух уравнений, решив которую относительно а и b, имеем
.
Подставляя эти коэффициенты в формулу (2), можно записать:
(3)
Члены уравнения (3), заключенные в скобки, называют функциями формы одномерного симплекс-элемента:
. (4)
С учетом обозначений (4) уравнение (3) принимает вид:
, (5)
или в матричной форме
, (6)
Скачать реферат