Теория управления. Принципы системного анализа

. (4д)

Аналогия уравнений типа (4) не является чисто формальной с точки зрения одинакового математического описания. Вероятно, за этой аналогией стоят скрытые закономерности, присущие природе в форме энергетических либо иных взаимных соответствий, тем более, что для всех рассмотренных подсистем между фазовыми переменными F и V существуют также аналогии для элементов типов L и R. Возвращаясь к элементу типа С, мы можем отметить, что С есть мера «емкости» или мера «инертности» при взаимодействии фазовых переменных в формах потока и потенциала, а точнее, при взаимосвязи потока со скоростью изменения потенциала. В механических подсистемах мерой инертности служит масса, в электрических и тепловых – емкость (теплоемкость). Изменение во времени потенциала (скорости движения в механических подсистемах, напряжения в электрической цепи, температуры при нагреве тела) приводит к изменению потока (движущей силы в механических системах, силы тока в электрических цепях, теплового потока при нагреве тел). Мерой взаимного соответствия этих изменений служит величина С. Чем больше емкость конденсатора, масса автомобиля, теплоемкость чайника с водой, тем труднее зарядить конденсатор до напряжения U, разогнать автомобиль до скорости v, нагреть воду до температуры Т.

Элемент типа L.Элемент типа L на эквивалентных схемах электрических и других подсистем изображают как катушку индуктивности (рис. 3, а). Для механических подсистем обычно используют условное обозначение пружины (рис. 3, б).

Компонентное уравнение для элемента типа L записывают в виде

(5)

где V, F – потенциальная и потоковая фазовые переменные.

В электрических подсистемах элемент типа L определяет индуктивность, при этом напряжение U связано с силой тока I зависимостью

. (5 а)

Для механических подсистем компонентное уравнение

(5 6)

может быть получено путем дифференцирования по времени уравнения пружины F= kx, где х – перемещение; k – жесткость пружины. В формуле (5, б) аналог электрической индуктивности L характеризует податливость пружины .

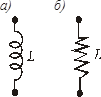
Рис. 3. Элемент типа L

Аналогичное компонентное уравнение можно получить для упругого стержня, используя закон Гука. При растяжении (сжатии) будем иметь

; (5 в)

при изгибе

; (5 г)

при кручении

(5 д)

где Е, G – модули упругости при растяжении и сдвиге; А – площадь поперечного сечения; J, Jk – моменты инерции при изгибе и кручении.

В гидравлических и пневматических подсистемах давление р идеальной жидкости (газа) связано с массовым расходом Q уравнением

(5 е)

где Lp – l/A зависит от длины трубопровода l и площади его поперечного сечения А. Для реальных жидкостей формула (5е) не учитывает массовые силы и гидравлическое сопротивление, которые могут быть учтены дополнительно

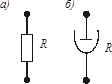
Элемент типа R. Условное графическое изображение элемента типа Rпоказано на рис. 4 для электрических (а) и механических (б) подсистем. Общее уравнение такого элемента имеет вид

F= V/R. (6)

В электрических подсистемах этому уравнению соответствует закон Ома

; (6 a)

в механических — уравнение вязкого трения:

(6 б)

где — величина, обратная коэффициенту вязкого трения;

в гидравлических — отмеченное выше гидравлическое сопротивление:

, (6 в)

где – аналог электрического сопротивления (v – кинематическая вязкость; d, l — диаметр и длина трубопровода);

в тепловых подсистемах:

(6 г)

где тепловой поток Ф и температура Т зависят от конвекционного сопротивления Rk.

Таким образом, во всех рассмотренных подсистемах можно установить аналогии фазовых переменных типа потока и потенциала (табл. 1).

Рис. Элемент типа R

Источники энергии и преобразователи. Аналоги топологических уравнений

Условное графическое изображение источников энергии типа Е и I показано на рис. 5.

На рис 6, а приведена схема трансформатора, имеющего математическую модель

(7)

где Т – коэффициент трансформации.

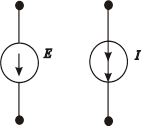
Рис. 5.Источники энергии

Примерами трансформаторов в механических подсистемах могут служить рычаги энергии и редукторы.

Гиратор (рис. 6, б) имеет модель

(8)

где G – коэффициент гирации.

Примером гиратора может служить гидроцилиндр, в котором давление Р преобразуется в силу F, действующую на поршень.

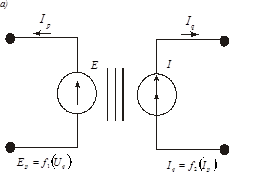
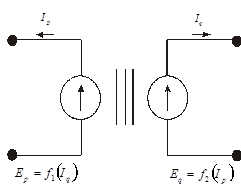
Рис. 6.Схемы трансформаторной (а) и гираторной (б) связи

Топологические уравнения типа (7), (8) в большинстве физических подсистем базируются на уравнениях равновесия и уравнениях неразрывности. Ниже рассмотрены аналогии топологических уравнений в подсистемах различной физической природы. Условимся снабжать индексом i элементы, примыкающие к данному узлу, а индексом j – входящие в данный контур, при этом в знаках суммы (∑) обозначения «» или «», где p, q – соответственно множество ветвей, примыкающих к узлу i и входящих в контур j, будем опускать.

Электрическая подсистема

Уравнения равновесия определяют равенство нулю суммы токов в узлах сопряжения элементов; их находят по первому закону Кирхгофа: