Теория управления. Принципы системного анализа

Его открытие называли по-разному, в том числе принципом Парето, законом Парето, правилом 80/20, принципом наименьшего усилия, принципом Дисбаланса.

Принцип 80/20 гласит, что небольшая доля причин, вкладываемых средств или прилагаемых усилий, отвечает за большую долю результатов, получаемой продукции или заработанного вознаграждения. Например, на получение 80% результатов, достигаемых в работе, у вас уходит 20% всего затраченного времени. Выходит, что на практике 4/5 приложенных вами усилий (немалая доля) не имеют к получаемому результату почти никакого отношения. Это, кстати, расходится с тем, чего люди обычно ожидают.

Введем на множестве D отношение предпочтения (обозначим его символом ). Будем говорить, что вектор предпочтительнее вектора , и писать , если среди равенств и неравенств имеется хотя бы одно строгое неравенство (рис. 6).

Аналогично на множестве DФ введем отношение доминирования: будем говорить, что векторный критерий оптимальности доминирует векторный критерий оптимальности , и писать , если .

Другими словами, объект доминирует объект , если по всем критериям предпочтительнее или эквивалентен , и хотя бы по одному критерию строго предпочтительнее. Объект называют доминирующим, а – доминируемым.

Если исключить из исходного множества доминируемые объекты, то останутся конкурирующие (эффективные).

Введенные отношение предпочтения и отношение доминирования являются транзитивными, т.е.

если и , то ;

если и , то

Выделим из множества DФ подмножество точек, для которых нет точек, их доминирующих. Множество , соответствующее , называется множеством Парето (переговорным множеством, областью компромисса) — рис. 7. Поскольку множество DФ на рисунке 7 является выпуклым, то множество - есть часть границы множества DФ — дуга AB, в которой точка A соответствует f1min, а точка B - f2min. Среди точек

,

нет более предпочтительных, поскольку

, но .

Таким образом, если , то .

Другими словами множество Парето можно определить как множество, в котором значение любого из скалярных (частных) критериев оптимальности можно улучшить только за счет ухудшения других частных критериев – любое из решений, принадлежащее множеству Парето, не может быть улучшено одновременно по всем частным критериям.

Альтернатива принадлежит множеству Парето, если она не хуже других по всем критериям и хотя бы по одному критерию лучше.

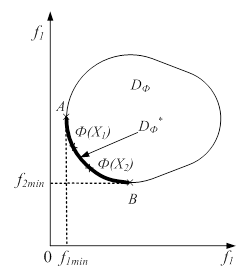
Рис. 8. Множество Парето

Для пояснения изложенного рассмотрим простейший метод, позволяющий приближенно находить множество Парето для случая двух критериев. На рис. 8, а построена область возможных значений в плоскости двух критериев. Исключение неэффективных точек в этом случае очень наглядно. Исключению подлежат все точки, образы которых в плоскости (f1, f2) расположены одновременно правее и выше образа исходной точки. В случае многих критериев геометрическая интерпретация аналогична.

После исключения неэффективных точек осталось всего 9 приближенно эффективных точек. Соединив их, получим приближенную компромиссную кривую E, которая вместе с точной компромиссной кривой D* построена на рис. 9, б. В качестве наилучшей среди исходной совокупности точек следует выбрать одну из этих 9 точек.

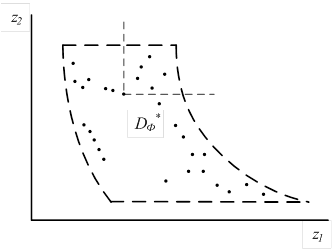а)

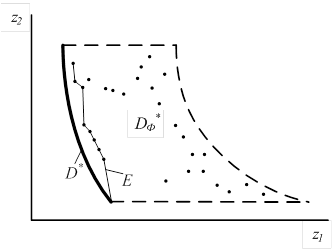б)

Рис. 9. Построение области Парето

Например, Андрей лучше всех решает задачи, а по остальным критериям не выделяется. Зато Вера, Галя, Ира, Катя, Лариса имеют высокие значения остальных критериев, так что они в среднем превосходят Андрея, причем Вера лучше всех по успеваемости, а по остальным критериям не хуже других студенток. Тогда Андрей обзятельно попадает в множество Парето, т.к. он уникальный (единственный) по первому критерию, а от группы студенток в множество Парето попадает один представитель – Вера, хотя остальные студентки превосходят Андрея по нескольким критериям (число критериев здесь не имеет значения).

Таким образом, поиск оптимального решения (точки) может осуществляться в соответствии с рисунком 10.

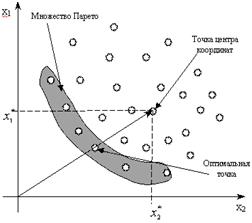
Рис. 10. Выбор оптимальной точки

18.4 Технологии отыскания эффективных решений

Суждения об относительной важности частных критериев ЛПР может выразить как в качественной, так и в количественной шкале. Если частные критерии измеряются в различных, а тем более разных по классам шкалах (количественных и качественных), их оценки не могут быть пересчитаны в некоторую объективную шкалу оценивания (например, в универсальный денежный эквивалент), то трудно представить, как соизмерить их относительную важность. А сделать это иногда требуется как можно быстрее и как можно адекватнее, чтобы можно было сразу представить себе ценность какой-то конкретной альтернативы. В подобных ситуациях, когда информацию об относительной важности требуется получить и использовать как можно быстрее и при этом обеспечить высокую адекватность и надежность суждений, более предпочтительным представляется учет относительной важности частных критериев в качественной шкале (так называемая «качественная информация об относительной важности»). К качественной информации об относительной важности частных критериев будем относить следующие вербальные суждения: