Теория управления. Принципы системного анализа

«критерий с номером i важнее критерия с номером j»;

«критерии с номерами s и t равноценны по важности».

Напрямую использовать информацию о превосходстве или равноценности для дальнейшего сокращения размера множества эффективных альтернатив и поиска наилучшего решения среди них можно только для некоторых частных случаев. Во-первых, это случай, когда шкалы всех частных критериев, относительно которых получена информация.

Второй частной ситуацией, когда возможно прямое использование качественной информации о равноценности или превосходстве в важности одних частных критериев над другими, является такая, в рамках которой фигурируют сообщения о равноценности всех критериев между собой, об абсолютно строгом (лексикографическом) упорядочении критериев по важности, а также о симметрически-лексикографическом упорядочении частных критериев по важности.

Самая сложная в получении, но и самая действенная – это информация об относительной важности критериев в количественной форме. Это информация о величинах замещений значений критериев между собой, о значениях коэффициентов важности частных критериев, количественная информация о допустимой степени взаимной компенсации значений тех или иных критериев, а также о виде функции агрегирования частных критериев в обобщенные критерии. В некоторых случаях такая информация поступает от ЛПР сразу. Но это – скорее исключение из правил. Значительно чаще количественную информацию приходится получать по частям.

Методы принятия решения при нескольких критериях

При необходимости ПР при многих критериях на практике обычно используют следующие подходы.

1. Свертка векторного критерия

Этот метод также называют скаляризацией векторного критерия или введением суперкритерия. Суть его заключается в следующем.

Выбираются коэффициенты βk ≥ 0 так, что функция

обобщила в себе" все требования частных критериев. При этом обычно

и каждый βk характеризует степень важности критерия fk(X).

На практике обычно ЛПР выбирает какие-то β1, …, βr, затем отыскивает наилучшую точку Х' – например, минимум S(X') при . Если при этом оказывается, что некоторые из значений ЛПР не удовлетворяют, тогда он корректирует значения β1, …, βr и решает задачу заново и т.д.

Рассмотренный подход также называют аддитивной сверткой. Он имеет существенный недостаток – трудно находить коэффициенты βk из-за разных размерностей критериев.

Этого недостатка лишена свертка вида:

или ,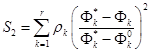

где – идеальное (реально недостижимое) значение k-го критерия, которое указывается ЛПР; – наименее предпочтительное для ЛПР значение k -го критерия; μk , ρk – весовые коэффициенты с тем же смыслом, что и βk. В двух последних свертках каждый k-й критерий выступает своим нормализованным значением , которое изменяется в пределах от 0 до 1. Данный подход снимает проблемы, обусловленные неодинаковыми размерностями входящих в свертку критериев.

Однако существуют и другие вопросы. В частности, можно показать, что выбор вида свертки влияет на конечный результат.

Для иллюстрации данного утверждения рассмотрим случай двух критериев Ф1 и Ф2 и предположим, что они оба получили одинаковые "веса": μ1 = μ2 =0,5 и ρ1 = ρ2 =0,5 . Пусть допустимая область в пространстве критериев имеет вид, представленный на рис. 11 а.

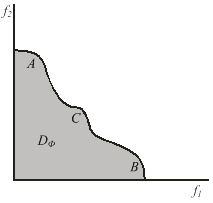
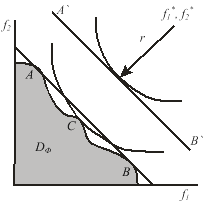
а) б)

Рис. 11 . Иллюстрация влияния вида свертки на конечный результат: а – допустимая область; б – линии равного уровня для критерия S1 (прямые) и S2 (окружности)

Для интегрального критерия типа S1 линии равного уровня представляют собой прямые, задаваемые уравнениями:

На рис. 11 б они показаны в виде линий АВ и A'B'. Для интегрального критерия типа S2 линии равного уровня – окружности с центром в точке , которые описываются уравнением вида:

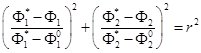
Из рис. 11 б видно, что первый тип рассматриваемой свертки предполагает выбор в качестве результата точки А или В; второй – точку С. Очевидно, что все три результата существенно отличаются друг от друга.

2. Оптимизация главного из нескольких критериев

При таком подходе один из критериев, наиболее важный с точки зрения ЛПР, оставляют в качестве единственного критерия, а все остальные заменяют ограничениями.

Пусть для определенности главным критерием считается f1(X). Тогда следует выбрать ограничения и рассмотреть задачу об отыскании минимума f1(X) при дополнительных ограничениях

При таком подходе возникает проблема выбора критериальных ограничений , что может потребовать выполнения специальных предварительных расчетов.

3. Последовательная оптимизация всех критериев

Сначала определяется минимальное значение f1(X) при . Обозначим его через . Выбираем "уступку" по этому критерию h1 и назначаем критериальное ограничение . Затем находится минимальное значение f2(Х) при и дополнительном ограничении . Получив значение и выбрав "уступку" h2, назначаем второе критериальное ограничение . После этого определяется минимальное значение f3(Х) при , и и т.д.