Таблица 2
|
№ опыта |
X0 |
X1 |
X2 |
Y |
|
1 |
2 |
3 |
4 |
5 |
|
1 |
+1 |
-1 |
-1 |
38 |
|
2 |
+1 |
+1 |
-1 |
68 |
|
3 |
+1 |
-1 |
+1 |
32 |
|
4 |
+1 |
+1 |
+1 |
62 |
Все дальнейшие вычисления полностью формализованы. Коэффициенты регрессии уравнения (3.2) определяют по формуле
![]() (3)
(3)
где xin – значение xi, в n-ом опыте;
N – число опытов;
уп – значение отклика в n-ом опыте.
Для вычисления коэффициентов регрессии по табличным данным достаточно перемножить данные столбцов у и соответствующих xi,сложить результаты и поделить их на число опытов.
Так, по данным табл. 2 будем иметь
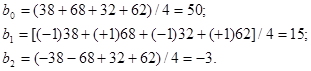
Искомое линейное уравнение поверхности отклика в закодированных переменных будет:
![]()
В натуральной (не кодированной) форме это уравнение имеет вид:
![]() (4)
(4)
Рассмотренный в примере план эксперимента соответствует двум факторам для линейной функции. Если поверхность отклика нелинейна, а вы пытаетесь представить ее приближенное выражение, то в уравнении регрессии (1) следует добавить член b12x1x2, учитывающий взаимодействие факторов х1 и х2. В нашем случае линейной исходной поверхности отклика этот член будет равен нулю, в чем нетрудно убедиться, добавив 6-й столбец, элементы которого равны произведениям элементов 3-го и 4-го столбцов.
В общем случае много факторного эксперимента уравнение регрессии имеет вид:
![]() (5)
(5)
Параметр b0 называют общим средним, параметры bi – главными эффектами (взаимодействиями нулевого порядка), параметры bij – эффектами взаимодействия первого порядка (эффектами двухфакторных взаимодействий), параметры bijk – эффектами взаимодействий второго порядка (эффектами трехфакторных взаимодействий) и аналогично b123 .n – эффектами взаимодействия порядка п-1 (эффектами n-факторных взаимодействий).
Наиболее часто используют два частных случая функции регрессии: линейную
![]() (6)
(6)
и неполную квадратичную
![]() (7)
(7)
Техника эксперимента с варьированием к факторов на двух уровнях сводится к проведению 2k опытов. Для построения матрицы планирования эксперимента при любом к следует дважды повторить матрицу планирования для случая к-1: один раз для нижнего уровня k-го фактора, а другой раз — для верхнего. Последовательность достраивания матриц планирования при увеличении к от двух до пяти показана в табл. 3. Первые четыре (отчеркнутые) опыта соответствуют двухфакторному эксперименту типа 22, повторяя табл. 2. Восьмифакторный план типа 23 дважды повторяет двухфакторный эксперимент при варьировании третьего фактора сначала на нижнем, а затем на верхнем уровнях. Аналогично строят планы полных факторных экспериментов при других значениях k.
Таблица 3
|
№ |
X0 |
X1 |
X2 |
X3 |
X4 |
X5 |
|
1 |
+1 |
-1 |
-1 |
-1 |
-1 |
-1 |
|
2 |
+1 |
+1 |
-1 |
-1 |
-1 |
-1 |
|
3 |
+1 |
-1 |
+1 |
-1 |
-1 |
-1 |
|
4 |
+1 |
+1 |
+1 |
-1 |
-1 |
-1 |
|
5 |
+1 |
-1 |
-1 |
+1 |
-1 |
-1 |
|
6 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
|
7 |
+1 |
-1 |
+1 |
+1 |
-1 |
-1 |
|
8 |
+1 |
+1 |
+1 |
+1 |
-1 |
-1 |
|
9 |
+1 |
-1 |
-1 |
-1 |
+1 |
-1 |
|
10 |
+1 |
+1 |
-1 |
-1 |
+1 |
-1 |
|
11 |
+1 |
-1 |
+1 |
-1 |
+1 |
-1 |
|
12 |
+1 |
+1 |
+1 |
-1 |
+1 |
-1 |
|
13 |
+1 |
-1 |
-1 |
+1 |
+1 |
-1 |
|
14 |
+1 |
+1 |
-1 |
+1 |
+1 |
-1 |
|
15 |
+1 |
-1 |
+1 |
+1 |
+1 |
-1 |
|
16 |
+1 |
+1 |
+1 |
+1 |
+1 |
-1 |
|
17 |
+1 |
-1 |
-1 |
-1 |
-1 |
+1 |
|
18 |
+1 |
+1 |
-1 |
-1 |
-1 |
+1 |
|
19 |
+1 |
-1 |
+1 |
-1 |
-1 |
+1 |
|
20 |
+1 |
+1 |
+1 |
-1 |
-1 |
+1 |
|
21 |
+1 |
-1 |
-1 |
+1 |
-1 |
+1 |
|
22 |
+1 |
+1 |
-1 |
+1 |
-1 |
+1 |
|
23 |
+1 |
-1 |
+1 |
+1 |
-1 |
+1 |
|
24 |
+1 |
+1 |
+1 |
+1 |
-1 |
+1 |
|
25 |
+1 |
-1 |
-1 |
-1 |
+1 |
+1 |
|
26 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
|
27 |
+1 |
-1 |
+1 |
-1 |
+1 |
+1 |
|
28 |
+1 |
+1 |
+1 |
-1 |
+1 |
+1 |
|
29 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
|
30 |
+1 |
+1 |
-1 |
+1 |
+1 |
+1 |
|
31 |
+1 |
-1 |
+1 |
+1 |
+1 |
+1 |
|
32 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
