Теория управления. Принципы системного анализа

Уровень критериев:

2. Исследовательская работа;

3. Рост;

4. Доходы;

5. Коллеги;

6. Местонахождение;

7. Репутация.

Уровень альтернатив:

8. А;

9. Б;

10. В.

Выполнение второго этапа связано с заполнением нижеприведенных таблиц по методу парных сравнений с применением шкалы относительной важности. В результате обработки таблиц получаем собственные вектора, которые определяют веса соответствующих дуг.

max = 6,35; ИС = 0,07; ОС = 0,06

В таблице пары критериев сравниваются с точки зрения их относительного вклада в общее понятие "удовлетворение работой". Задавался вопрос: который из заданной пары критериев представляется вносящим больший вклад в понятие "удовлетворение работой" и насколько? Например, число 5 в третьей строке и четвертом столбце показывает, что "доходы" намного важнее, чем "общество коллег".

В следующей таблице представлены результаты парных сравнений относительно соответствующих критериев.

Результатом третьего этапа (синтеза) является определение весов согласно соотношению (9). Так как уровень 1 имеет одну цель, то Z1 = 1. Отсюда:

Z2 = 21Z1 = 0,16;

Z3 = 31Z1 = 0,19;

Z4 = 41Z1 = 0,19;

Z5 = 51Z1 = 0,05;

Z6 = 61Z1 = 0,12;

Z7 = 71Z1 = 0,30;

Вычислив веса критериев, переходим к вычислению весов альтернатив (т.е. объектов третьего уровня):

Z8 = 82Z2 + 83Z3 + 84Z4 + 85Z5 + 86Z6 + 87Z7 = 0,160,16 + 0,330,19 + 0,450,19 + 0,770,05 + 0,250,12 + 0,690,3 = 0,45

Z9 = 92Z2 + 93Z3 + 94Z4 + 95Z5 + 96Z6 + 97Z7 = 0,590,16 + 0,330,19 + 0,090,19 + 0,050,05 + 0,050,12 + 0,090,3 = 0,25

Таким образом, в конечном счете альтернатива А имеет вес 0,45, Б - 0,25 и В - 0,3.

Пример 2

Задача определения приоритетов отраслей промышленности. Она возникает при распределении энергии для нескольких крупных потребителей в соответствии с их общим вкладом в реализацию различных целей общества. Иерархия решения этой задачи имеет следующий вид:

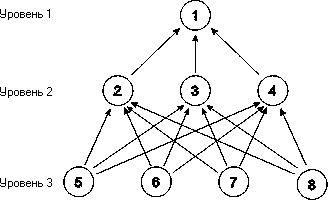
Рис. 18. Иерархия задачи определения приоритетов отраслей промышленности

Первый уровень иерархии имеет одну цель: общее благосостояние страны (1).

Второй уровень иерархии имеет три цели: сильная экономика (2), здравоохранение (3) и национальная оборона (4). Приоритеты этих целей получаются из таблицы парных сравнений относительно цели первого уровня.

Объектами третьего уровня являются отрасли промышленности (5,6,7,8). Задача заключается в определении влияния отраслей промышленности на общее благосостояние страны через промежуточный второй уровень.

Пример 3

Применение МАИ для сравнительного анализа различных технических систем. Например, необходимо осуществить оценку четырех современных систем аккумулирования энергии на основе шести критериев. Соответствующая иерархия имеет следующий вид:

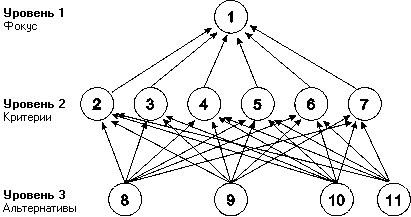
Рис. 19. Иерархия сравнительного анализа технических систем

В таблице представлены результаты парных сравнений относительно соответствующих критериев.

В качестве критериев принимались следующие:

2. Экологический.

3. Экономический.

4. Социальный.

5. Выбор места.

6. Время, требуемое для постройки.

7. Совместимость с энергосистемой.

Множество систем аккумулирования энергии включало:

8. Накопление сжатого воздуха.

9. Подземная гидроаккумуляция.

10. Электрические батареи.

11. Накопление энергии водорода.

Матрица парных сравнений к примеру 3

max= 6,05; ИС = 0,01; ОС = 0,01.

После проведения этапа синтеза получено следующее ранжирование аккумулирующих систем:

-электрические батареи - 0,36;

-накопление сжатого воздуха - 0,26;

-накопление энергии водорода - 0,24;

-подземная гидроаккумуляция - 0,14.

Лекция 15. Метод конечных элементов

Общий ход решения задачи на основе метода конечных элементов

Решение задач анализа при функциональном моделировании сводится к определению вектора V, который удовлетворяет исходным уравнениям задачи и граничным условиям. Часто искомую функцию задают в виде ряда

(1)

где – базисные функции от независимых переменных,

– неизвестные постоянные коэффициенты.

Методы определения постоянных коэффициентов весьма разнообразны. Так, в методе Ритца их находят из условия минимума потенциальной энергии системы, в методе коллокаций – из условия удовлетворения дифференциальных уравнений задачи в отдельных точках и т. д. Выбор базисных функций в конечном счете определяет успех решения задачи: если эти функции подобраны удачно, решение получается простым, в противном случае приходится удерживать большое число членов ряда (9.1), что существенно затрудняет расчет и не всегда приводит к желаемым результатам. Для простых случаев разработаны рекомендации по выбору базисных функций, в сложных случаях проблема назначения этих функций может оказаться не проще решения неходкой задачи.