Теория управления. Принципы системного анализа

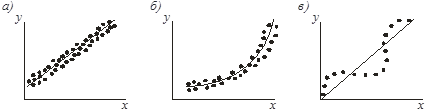
Рис. 2.Диаграммы разброса

Задачу подбора вида функции, наилучшим образом соответствующей конфигурации кривой, называют подгонкой кривых по точкам. Для этой цели используют графические изображения наиболее характерных функций, некоторые из которых показаны на рис. 3.

ри подгонке кривых по точкам прежде всего следует определить количественный принцип соответствия теоретической функции экспериментальным точкам. В качестве меры такого соответствия было бы логичным принять минимальные отклонения по всем точкам, т. е. суммы всех отклонений. Но поскольку отклонения теоретических значений от экспериментальных могут быть положительными и отрицательными, то с математической точки зрения проще предварительно возвести эти отклонения в квадрат и обеспечить минимум для суммы квадратов отклонений. Этот метод, названный методом наименьших квадратов, соответствует критерию наилучшего приближения.

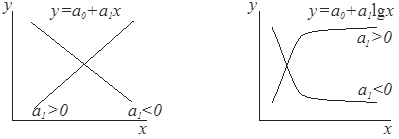
а)

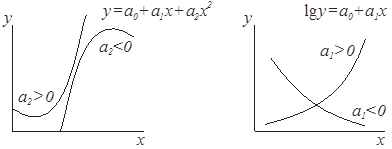
б)

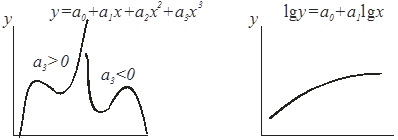
в)

Рис. 3. Различные виды регрессионных кривых

Для поиска математических зависимостей между переменными по накопленным экспериментальным данным обычно используют методы регрессионного и корреляционного анализов. Регрессионный анализ дает возможность построить по экспериментальным данным уравнение, а корреляционный анализ позволяет судить, насколько хорошо экспериментальные точки согласуются с выбранным уравнением, а также насколько тесна связь между двумя и более величинами, наблюдаемыми ификсируемыми при моделировании.

Регрессионный анализ. Математический метод, обеспечивающий такую подгонку выбранной кривой, при которой экспериментальные точки описывают ее наилучшим образом в смысле критерия наименьших квадратов, называют регрессионным анализом.

Корреляционный анализ.Наилучшее приближение теоретической кривой к экспериментальным данным еще не означает, что реально существующая физическая зависимость соответствует именно этой кривой. Наглядный этому пример дает рис. 3, в. Описание экспериментальных точек прямой линией вполне соответствует методу наименьших квадратов, но не соответствует физической сущности явления, если мы не постулируем приближенное представление последнего в линейной постановке.

Для оценки согласованности экспериментальных точек с теоретическими прогнозами используют понятие корреляции. Если регрессия определяет эту согласованность по форме, то корреляция показывает, насколько точно она отражает действительность. Вместе с тем корреляция между переменными означает лишь то, что их изменения взаимосвязаны, однако это еще не доказывает наличие причинно-следственной связи между переменными.

Мерой корреляционной связи между переменными X a Y служит коэффициент корреляции rху, представляющий собой отношение корреляционного момента (математического ожидания произведения отклонений X и Y) к произведению средних квадратических отклонений этих величин

Для случая простой линейной регрессионной задачи (т.е. для случая, когда имеются одна зависимая и одна независимая переменные, связанные между собой линейно) коэффициент корреляции вычисляют по формуле

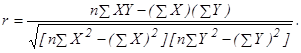(2)

Коэффициент корреляции лежит в пределах от -1 до +1. Коэффициент корреляции, равный нулю, соответствует полному отсутствию корреляции (рис. 4, а). При наличии слабой (схема б) или сильной (схема в) положительной корреляции коэффициент корреляции соответственно равен +1 или близок к нему. Если этот коэффициент равен - 1, то имеет место сильная отрицательная корреляция (схема г).

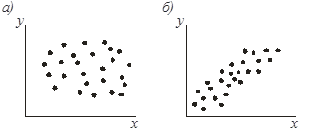
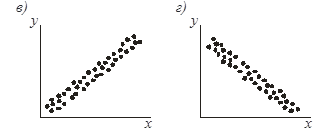
Рис. 4. Виды корреляции

Лекция 12. Методы получения регрессионных уравнений

Полный факторный эксперимент

Изложение основ факторного планирования эксперимента начнем с простейшего примера.

Пусть имеется две входные переменные Х1 и Х2, одна из которых в интересующей нас области, заштрихованной на рис. 1, а, изменяется в пределах 0,4X10,8, а другая — в пределах 10X230. В процессе проведения эксперимента найдены значения ординат поверхности отклика в граничных точках (рис. 1, а), приведенные в табл. 1.

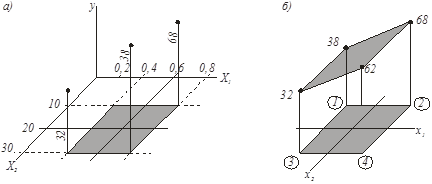
Рис. 1.Полный факторный эксперимент

Поставим задачу поиска аналитического выражения функции отклика в линейной постановке, т.е. дадим приближенное представление этой функции в виде:

(1)

Таблица 1

Для формализации процедур обработки экспериментальных данных факторы удобно представлять в закодированном виде. С этой целью выберем новую систему координат x1 х2 у (рис. 1, а, 6), начало которой совместим с центром интересующей нас области, и назначим масштабы по осям факторов так, чтобы нижний уровень фактора соответствовал - 1, а верхний +1. Это легко достигается с помощью преобразований вида

(2)

где xi – кодированное значение i-ro фактора;

Хi – натуральное значение фактора;

Хо – нулевой уровень;

– интервал варьирования фактора.

Для фактора Х1 нулевой уровень и интервал варьирования будут равны

X10=(0,4+0,8)/2=0,6; X1 = (0,8-0,4)/2=0,2. Для фактора Х2 имеем: X20=(10 + 30)/2=20; X2 = (30-10)/2=10.

Кодированные значения факторов приведены в табл. 3.2.

В первом и пятом столбцах этой таблицы повторены значения табл. 1. Во втором столбце приведены значения фиктивной переменной x0, характеризующей свободный член bо в уравнении регрессии (1). Значения x0 всегда принимают равными +1. В 3 и 4 столбцах записаны искомые кодированные переменные; так, для фактора Х1 в первой точке кодированное значение будет x11=(0,4 - 0,6)/0,2= - 1. Подобные таблицы называют матрицами планирования полного факторного эксперимента.