, (22)
где матрица жесткости К будет равна
(23)
Матрица жесткости (23) конечного элемента не зависит от действующих на элемент нагрузок и поэтому остается неизменной для всех нагружений. Элементы этой матрицы представляют собой коэффициенты канонических уравнений метода перемещений для расчета одного конечного элемента.
Рассмотрим объединение конечных элементов в ансамбль на примере простейшей сети из трех конечных элементов (рис. 5).
Для каждого конечного элемента мы можем записать формулу (17), заменяя узлы 
конкретными номерами. Так, для первого элемента
.
Поступая аналогично с остальными узлами, получим:
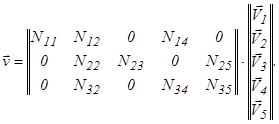(24)
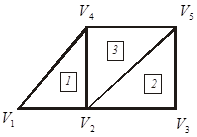
Рис.5.Ансамбль трех конечных элементов
Напомним, что узловые значения искомой функции
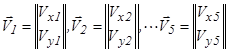
пока еще не известны и подлежат определению. С этой целью нужно использовать какой-нибудь принцип, выражающий физическую сущность задачи. В задачах строительной механики таким принципом могут быть уравнения равновесия с учетом совместности перемещений. Когда мы все это проделаем, задача будет решенной, поскольку формулы (20), (21), (24) с учетом обозначений (18), (19) позволяют определить в любой точке области нормальные и касательные напряжения, найти угловые и линейные деформации, вычислить перемещения данной точки в направлении осей х и у. Совокупность указанных формул, полностью определяющих поведение исследуемой системы, составляет ее математическую модель.
Перейдем к объединению конечных элементов в ансамбль.
Пусть в узлах системы конечных элементов действуют внешние силы, определяемые вектором
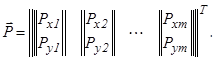(25)
К каждому i-му узлу сети примыкает в общем случае 
конечных элементов, каждый из которых вносит свой вклад в матрицу жесткости. Поэтому для каждого i-го узла суммарная матрица жесткости будет представлять собой сумму элементов матриц жесткости всех примыкающих к узлу элементов, т.е.
, (26)
в то время, как узловые перемещения для всех этих элементов будут общими в силу совместности перемещений всех элементов, соединенных в i-м узле. Поскольку узлы имеют две степени свободы, вектор перемещения i-го узла будет содержать две компоненты перемещений 
точно так же, как внешняя сила [см. формулу (25)] имеет две компоненты Pxi, Pyi. Совокупность перемещений всех m неопорных узлов сети конечных элементов определится m-мерным вектором перемещений:
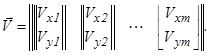(27)
Общую матрицу жесткости для всей конструкции можно выразить в виде
. (28)
Окончательная зависимость между вектором сил (25) и вектором перемещений (27) будет иметь вид
. (29)
Таким образом, вектор узловых значений искомой функции будет равен
. (30)
Лекция 16. Аналитические модели сложных систем
Основные понятия
Математическое моделирование позволяет устанавливать зависимости выходных (y1, у2, ., уn) переменных от входных переменных (x1, x2 , ., хn) при целенаправленном изменении внутренних параметров (h1, h2, ., hn) с учетом в ряде случаев воздействия внешней среды. Наиболее просто эта задача решается, если известна функциональная зависимость между соответствующими многомерными векторами:
(1)
В таком виде математическую модель удается получить только для очень простых ситуаций. В обычных условиях математическое описание процессов в исследуемом объекте задают в форме системы дифференциальных уравнений. Понятно, что ЭВМ не может непосредственно оперировать даже с простейшими зависимостями типа (1), поэтому построение математических моделей подразумевает комплекс преобразований этих зависимостей до уровня, допускающего численное решение, и последующую реализацию такого решения на основе программ анализа в виде элементарных арифметических и логических операций.
В простейших ситуациях исходная задача может быть представлена системой линейных алгебраических уравнений, которая легко сводится к последовательности элементарных операций (ПЭО) на основе стандартных процедур с использованием библиотечных программ. Если модель задана системой нелинейных алгебраических уравнений, то возможны либо непосредственный переход к ПЭО, либо предварительная линеаризация с дальнейшим переходом к ПЭО (рис. 1).
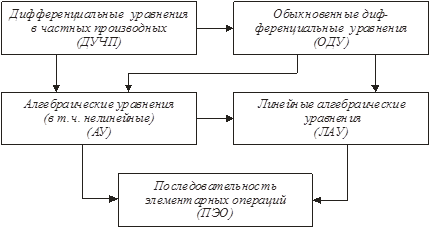
Рис. 1.Преобразования уравнений при построении аналитических моделей
Наиболее типичными являются модели, в которых исследуемый процесс описывается обыкновенными дифференциальными уравнениями или дифференциальными уравнениями в частных производных. Численные решения таких уравнений основаны на дискретизации переменных или алгебраизации задачи. Дискретизация заключается в замене непрерывных переменных конечным множеством их значений в заданных для исследования интервалах, а алгебраизация – в замене производных алгебраическими соотношениями, Если дифференциальные уравнения в частных производных описывают статическое состояние, то дискретизация и алгебраизация преобразуют дифференциальные уравнения в систему алгебраических уравнений, в общем случае нелинейных. Так, если рассматриваются переменные, изменяющиеся в пространстве и во времени, то при решении задачи на первом этапе устраняются производные по пространственным координатам, что позволяет перейти к обыкновенным дифференциальным уравнениям, а затем – производные по времени с переходом к алгебраическим уравнениям. Дальнейшее решение задачи может выполняться на основе метода простых итераций, либо быть сведено к предварительной линеаризации на основе метода Ньютона с переходом к линейным алгебраическим уравнениям. Решение системы таких уравнений выполняется с помощью прямых методов, например, метода Гаусса.
Ниже рассмотрена цепочка последовательных преобразований, которая позволяет однотипными приемами решать различные задачи. За базовое принято численное решение дифференциальных уравнений первого порядка с заданными начальными условиями (задача Коши) и системы таких уравнений. К подобным уравнениям может быть приведено обыкновенное дифференциальное уравнение n-го порядка. Дифференциальное уравнение с заданными граничными условиями может быть представлено как редукция к задаче Коши и тем самым решено аналогичными способами.
Скачать реферат