Зонирование территории по степени риска цунами

В связи с этим ставится задача нахождения компромиссного решения, поиск которого можно осуществить различными путями. На практике предпочтение обычно предпочтение отдают следующим трем способам [1].

Производится ранжирование критериев, то есть расположение их в порядке важности. Затем приступают к поиску решения оптимального по наиболее важному из них. После этого задавшись допустимой величиной изменения первого критерия, ищут решение по второму критерию в полученной области и т.д.

Формируется единый (интегральный) критерий, например, путем суммирования произведений имеющихся критериев на весовые коэффициенты (коэффициенты важности).

Все критерии кроме одного превращаются в ограничения.

Однако к анализу многокритериальных задач можно подойти и с другой позиции: попытаться сократить множество исходных вариантов, т.е. исключить из неформального анализа те варианты решений, которые заведомо плохи.

Принцип Парето-оптимальности

Рассмотрим один из путей определения множества оптимальных решений, предложенный итальянским экономистом Парето [2].

В ряде случаев (обычно при отсутствии дополнительной информации о важности критериев) оптимумом по векторному критерию считают множество Парето-оптимальных векторов. Это означает, что на множестве векторных оценок вводится отношение строгого предпочтения - отношение Парето: векторная оценка более предпочтительна по Парето-отношению, чем , если справедливы неравенства , , и среди этих неравенств найдется хотя бы для одного значения строгое неравенство .

Векторную оценку , для которой не существует более предпочтительной по Парето-отношению, называют Парето-оптимальной, а также эффективной, или неулучшаемой по векторному критерию . Множество всех таких оценок называют эффективными, или множеством Парето. Соответственно точку называют Парето-оптимальной или эффективной.

Приведем пример, поясняющий определение множества Парето. Предположим, что цели проблемы определяются двумя однозначными функциями:

Тогда каждому допустимому значению переменной х отвечает одна точка на плоскости , и равенства , определяют параметрическое задание некоторой кривой abсd в этой плоскости (рис.1.3). К множеству Парето относится не вся кривая. Так, участок bс, очевидно, не принадлежит этому множеству. На этом участке изменению переменной х отвечает одновременное увеличение обеих целевых функций и, следовательно, такие варианты решений должны быть сразу исключены из дальнейшего рассмотрения.

Из этих же соображений должен быть исключен участок a'b, поскольку для каждой его точки е найдется точка, принадлежащая участку cd, в которой значения функций и больше, чем в точке е. Следовательно, к множеству Парето могут принадлежать только участки аа’ и cd, причем точка а’ должна быть исключена.

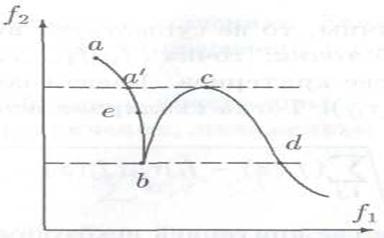
Рис.1.3 Кривая возможных выборов на плоскости критериев .

Понятие эффективных точек играет большую роль при многокритериальной оптимизации: оптимальное решение разумно выбирать среди эффективных точек, так как векторную оценку такого решения улучшить одновременно по всем критериям принципиально невозможно.

Таким образом, в ряде случаев выделение множества эффективных точек (или множества Парето) является первым этапом решения многокритериальной задачи.

Алгоритм построения множества Парето

Численные методы построения множества Парето

Задача выделения всех эффективных точек в общем виде еще не решена, но разработано довольно много различных методов отыскания эффективных точек для двухкритериальных и линейных многокритериальных задач [4].

Рассмотрим простейший случай (два критерия). Имеем задачу:

(2.1)

Каждой точке соотношения

(2.2)

ставят в соответствие некоторую точку в плоскости критериев. Соотношения (2.2) определяют отображение множества на .

Множество носит название множества достижимости. Множество Парето представляет собой лишь часть границы множества достижимости.

Приближенное построение множества Парето сводится к последовательному решению задач математического программирования. Опишем одну из возможных схем расчета.

Фиксируем некоторые желательные значения критериев и :

Значения C1 и С2 следует выбрать так, чтобы они принадлежали множеству достижимости. Теперь решаем две оптимизационные задачи:

1)

2)

Решив эти задачи, определим точки а и b (рис.2.1). Проведя через них прямую 1, получим простейшую аппроксимацию множества Парето. Для уточнения аппроксимации решаем следующие задачи:

3)

4)

Находим еще две точки - c и d, принадлежащие этому множеству. Значения С3 и С4 снова должны принадлежать множеству достижимости.

Через точки а, с, d и b проводим ломаную 2, которая будет следующим приближением. Очень часто подобной информации о структуре множества Парето уже бывает достаточно для решения практических задач.

Если множество Парето выпукло, то, увеличивая количество точек, которые определяются описанным способом, строим многогранник, аппроксимирующий это множество с любой степенью точности. Однако практика дает примеры множеств Парето, которые не являются выпуклыми. Тогда задача их аппроксимации резко усложняется.